講解完基本知識之後，開始介紹具體模型的部分，搭配範例可以更有感覺的知道實際上 AI 是怎麼做預測的。

接下來的範例，資料有的是機器學習用的公開資料，有的是為了方便解說的虛擬資料，可以從範例的程式碼作確認，就不另加說明。數學的部分不作深度的討論，但會介紹為了什麼目的而使用，順著說明看下去即可。

線性回歸（Linear Regression）

假設輸入和輸出是呈現類似一條直線的線性關係。
試著畫一條直線穿過這些資料。並用這條直線函數預測未知答案。

比如說使用同一個班級男生的身高和體重分布，來預測這個班級 185 公分的男生體重可能為多少。

部分資料：

先確認身高是否真的會影響體重，下面是透過程式產生的相關係數列表，可以看出我們持有的身高和體重資料有9成的正相關，代表身高和體重非常有關係，而身高就是我們人為挑出的特徵，體重是我們的標籤。

直接從圖形也能看出是否有相關性：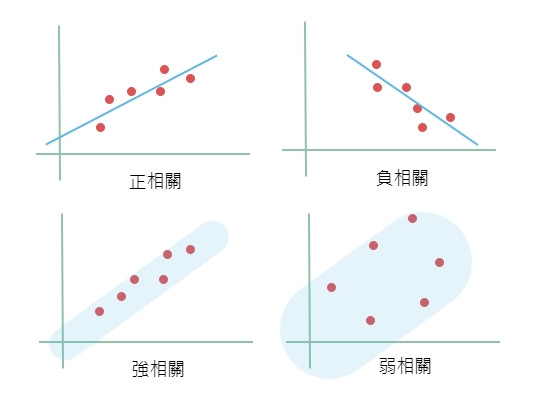

因為是預測體重，所以其他人的身高可以當做特徵資料（x），體重可以當相對應的答案（y）。

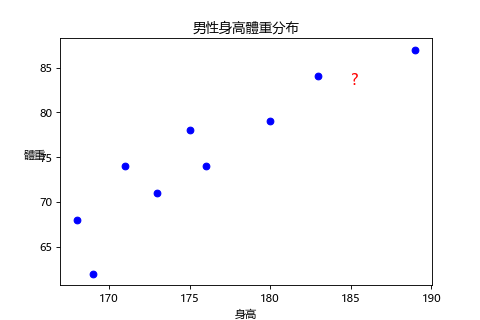
這條最能代表資料的直線是怎麼算出來的呢？我們可以透過國中學過的直線方程式：
（w這邊是指斜率，b是截距）
透過不同的 w 和 b 去畫一條直線，計算這條線的 y 和實際答案的 y 之間的誤差加總起來是否為最小，如果不是就換下一條線，這個求誤差的方法我們稱為損失函數（Loss Function）。

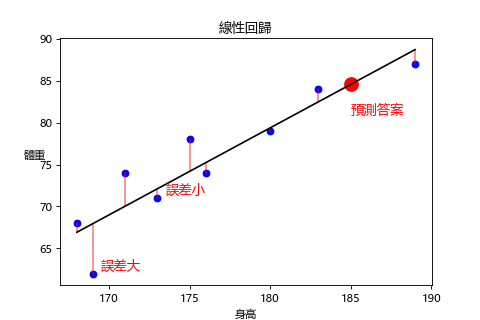
我們也可以把線拉成水平直接看誤差大小。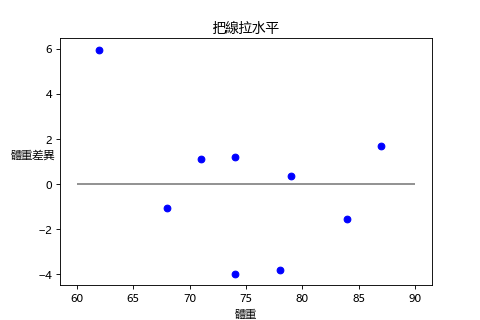

損失函數有很多種，線性回歸因為誤差有的為正有的為負，所以每個誤差取平方通通變正再加總取平均就是這條線和所有實際答案的誤差值。這個平方後加總取平均的算法叫做均方誤差（簡稱 MSE，Mean Square Error），而線性回歸如何找到最小誤差的那條線有一個公式可以用，我們稱作最小平方法（簡稱 OLS，Ordinary Least Squares）。

所以簡單說線性回歸的步驟就是

1. 決定模型：使用直線方程式這個函數，w 和 b 此時是未知的參數（Parameter）。
2. 算誤差（決定一個損失函數）：這邊使用均方誤差代入各種 w 和 b可以算出預測 y 和實際 y 的誤差。
3. 最小化損失函數（又叫最佳化，optimization）：用最小平方法找出讓誤差最小的參數 w 和 b 的確切數值。

機器學習就是這三個步驟。1. 和2. 要決定模型函數和誤差怎麼算，而 3. 最佳化通常是透過數學去逼近一個最佳的解。　

學習完的模型，也就是我們找到這條線的 w 和 b 確切數值的函數：
y = 1.03664 * x - 107.22803
將 x 代入185，y = 84.55

185 公分的男生體重預測為 84.55 公斤。

多項式回歸

如果輸入和輸出關係不像是一條直線那怎麼辦呢？那就不透過直線方程式，而是拉一條曲線來盡可能貼近這些資料。

專業一點的講法叫擬合（fitting）這些資料。

這個曲線可以用 n 次多項式來處理， 所以這個方法叫多項式回歸。比如說 x 取到 2 次方

或是取到 3 次方

次方越高越擬合，也就是對資料的誤差就越小，但是太擬合也會有問題，沒辦法反映真實的傾向。這種狀況我們叫做過度擬合（Overfitting），或叫過度學習。

簡單來說我們使用已知資料找到預測的方法，最終還是要看對未知資料能否做出準確的預測，對已知資料的誤差小，但是對未知的資料誤差大的話就是過度擬合。

我們透過已知資料取到 2 次方的話預測線長這樣，雖然和已知資料的誤差可能有點大，但預測出來的趨勢和想要預測的未知資料還蠻接近的。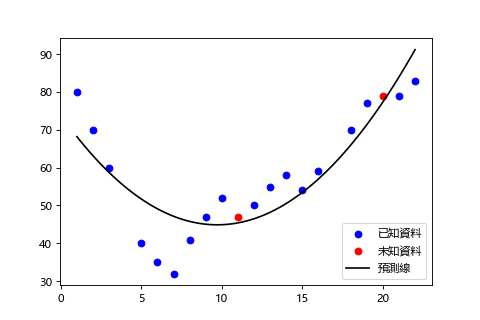

取到 11 次方的話，變成硬是把預測線拉過去貼住已知資料而已，雖然對已知資料的誤差變小了，反而無法對真正想預測的未知資料做出好的預測。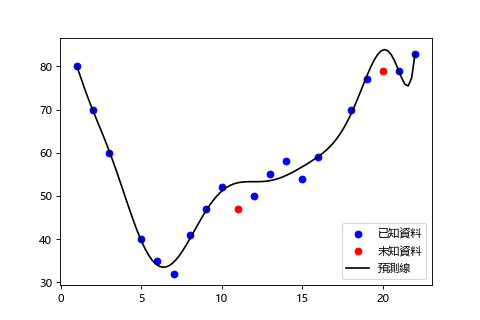

過度擬合是機器學習非常重要的問題，如何解決，後面會介紹。這邊只要知道太擬合不是一件好事就行了。

邏輯回歸（Logistic Regression）

線性回歸的分類版。畫出一條直線區隔出二種類型做分類。

雖然名字有回歸但不能做回歸問題。只能做分類問題。

這次想使用兩個特徵，透過乳房的腫瘤資料來判斷是普通的良性腫瘤還是惡性腫瘤（癌症）。

部分資料：

腫瘤紋路是指照片上不同程度的灰色數值，常用來做腫瘤判斷。

先來確認腫瘤資料的相關係數：

我們想要預測是否為乳癌，所以乳癌的有無就是要預測的答案 。而作為特徵的腫瘤大小和腫瘤紋路這兩個資料彼此之間的相關性不大，個別對乳癌的負相關也還算強，拿來當特徵沒有問題。

也可以用圖確認相關分布，看得出來使用這兩個特徵可以容易區分出乳癌的有無（兩個類別沒有混在一起）。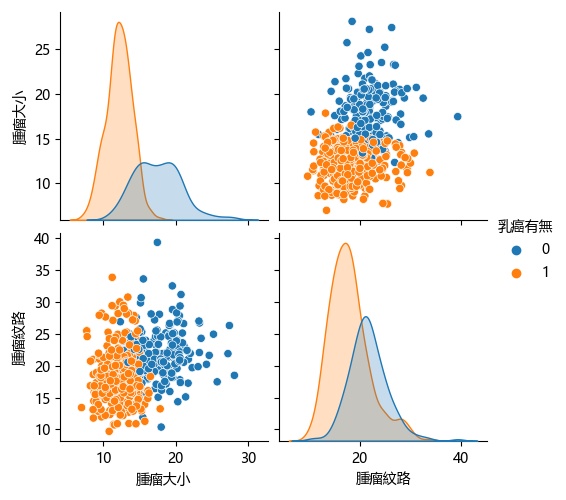

邏輯回歸主要使用 sigmoid 函數（又叫邏輯函數）將任何數值轉換成 0 到 1 之間代表發生的機率。

• x 越大，y 越接近 1。
  因為 x 越大 就越小，1除上（一個非常小的數加上1） 就越接近1 。
• x 越小，y 越接近 0。
  因為 x 越小就越大，1除上（一個非常大的數加上1）就越接近0。

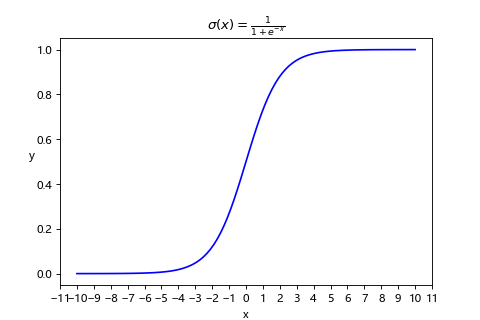
而透過設定門檻（或稱閥值，比方說 0.5）可以將閥值以下視為0，閥值以上視為 1來做二種類型（有・無）的分類。

交給程式做計算：

1. 決定模型：使用 sigmoid 函數做分類。
2. 算誤差（決定一個損失函數）：利用對數損失函數（Logarithmic Loss Function）。
3. 最小化損失函數（最佳化）：使用最大概似估計（MLE，Maximum Likelihood Estimation），找出特定的參數數值可以使資料 x 預測出 y 的概率最高。

學習完的模型，也就是我們找到 sigmoid 確切數值的函數：

將 腫瘤大小 15 代入，腫瘤紋理 25 代入 , y = 1 (良性)

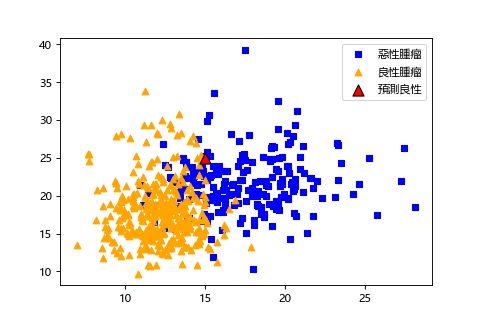
大小 15，紋路 25 的腫瘤預測為良性腫瘤。但是令人在意的準確率如何呢？我們會在評價模型時介紹怎麼做確認。

最後用來做分類的直線長這個樣子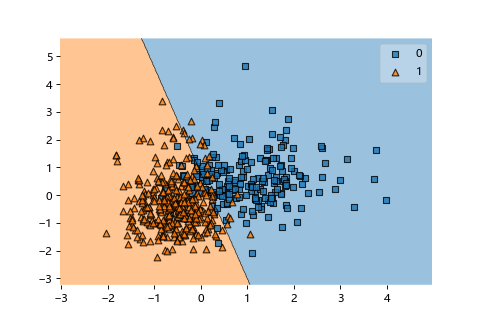

K 近鄰（簡稱 KNN，K-Nearest Neighbor）

白話一點就是你最近的 K 個鄰居。根據資料彼此之間的距離進行分類，距離哪一種類別最近，就分到哪一類，所以 KNN 常被用於分類問題。

簡單說你最要好的幾個朋友是什麼類的人，你就是什麼類的人。很像是成語的一丘之貉「近朱者赤，近墨者黑」。

KNN 的演算法步驟如下：

1. KNN 中的 K 代表找出距離你最近的 K 筆資料進行分類。
   （你最要好的K個朋友），比如說 k=3
   
2. 當這 K 筆資料被選出後，就以多數決的方式分到那一個類別。
   （這些朋友當中哪一類的人最多，你就是那一類的人）
   

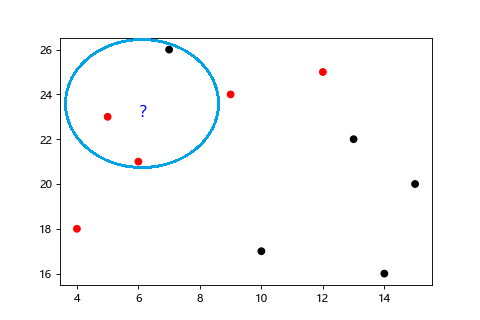
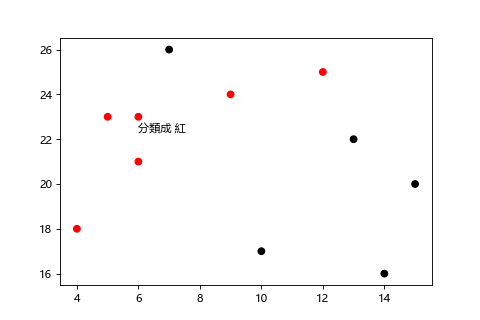
K通常會取奇數，以避免多數決沒法判斷，資料如果太偏向某一類別也很難做分類。

補充資料

• 範例程式 - 線性回歸
• 範例程式 - 多項式回歸
• 範例程式 - 邏輯回歸
• 範例程式 - KNN
• 線性回歸的特徵如果不只一個時，可以使用多元線性回歸（Multiple regression）
• 如果要分類兩個以上的類別，會使用 Softmax 函數，後面會介紹。

立即複習

• 線性回歸建立模型使用的函數叫做？使用的損失函數為何？
• 多項式回歸建立模型使用的函數叫做？
• 邏輯回歸建立模型使用的函數叫做？
• 附近都是某個類別，自己就被歸在那類的演算法叫做？

參考資料

• MACHINE LEARNING 2021 SPRING
  ※機器學習的3步驟概念出自台大李宏毅老師的機器學習課程。
• PYTHONとRPAで遊ぶ
• W3C School - Polynomial Regression